Currently a rough approximation to the Earth's orbit is 0.983 x 1.017 AU x 0.00 deg in ecliptic coordinates (an AU is 149.6 million km, the mean distance of the Earth from the Sun, and the ecliptic plane is the mean plane of the Earth's orbit). The small extra speed of SIRTF compared to the Earth will change SIRTF's heliocentric orbit to about 0.996 x 1.019 AU x 1.14 deg with a year about 4 days longer than Earth's. Most of the energy goes into the small inclination change, but the higher average distance from Earth means that SIRTF moves more slowly around the Sun, until by a year after launch SIRTF trails Earth by 10 million km. By Kepler's second law, the slowest point in each orbit is the aphelion (farthest point from the Sun). The aphelic velocities of SIRTF and Earth are almost the same, but SIRTF will be at its aphelion - and thus slowest speed - at launch, while Earth is just past its aphelion and starting to speed up again. This means that SIRTF will start falling behind the Earth right away. To achieve this, the Delta must fire to give SIRTF speed backwards and outwards relative to the Earth's motion.
[Note for those who, like me, know just enough orbital mechanics to be dangerous: decreasing the velocity around the Sun would normally reduce the orbital period. While SIRTF is still near the Earth, the fact that the Earth is just ahead of it and tugging on it helps to increase SIRTF's angular momentum relative to the Sun. By the time SIRTF leaves the Earth's gravitational sphere of influence, it is just enough further out from the Sun that the larger distance compensates for the smaller tangential velocity in producing larger total angular momentum and thus orbital period.]
SIRTF's orbit is called an 'Earth-trailing orbit'; it has the advantage that the infrared-bright Earth is nice and small, so doesn't block out large interesting pieces of the sky SIRTF might want to look at. Also, the total velocity change needed from parking orbit to get to a distant circular orbit around the Earth by going to transfer orbit and then burning again to circularize is more than the velocity change needed for escape, letting you use a smaller rocket. On the other hand, after a number of years SIRTF will be so far from Earth it will drift out of communications range - but by then its helium will have run out anyway.
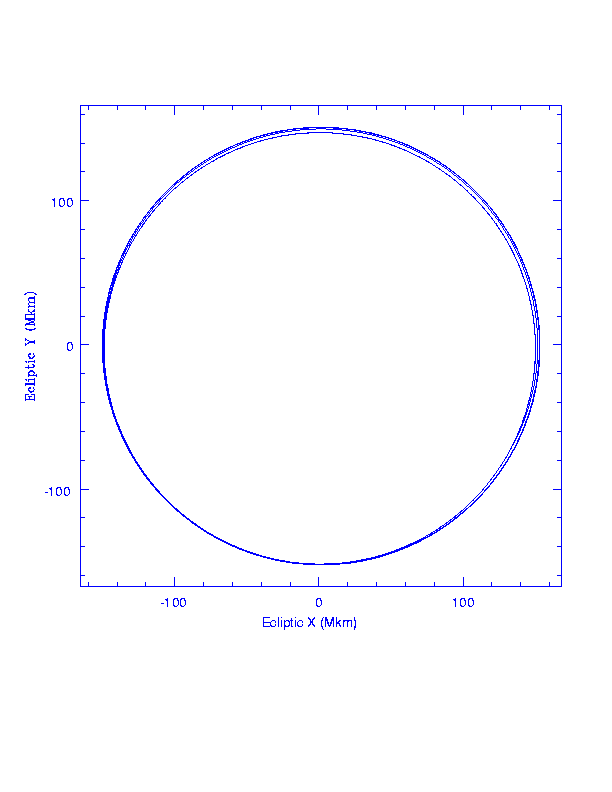
SIRTF's orbit in an inertial frame centered on the Sun, in ecliptic coordinates, is very close to Earth's.

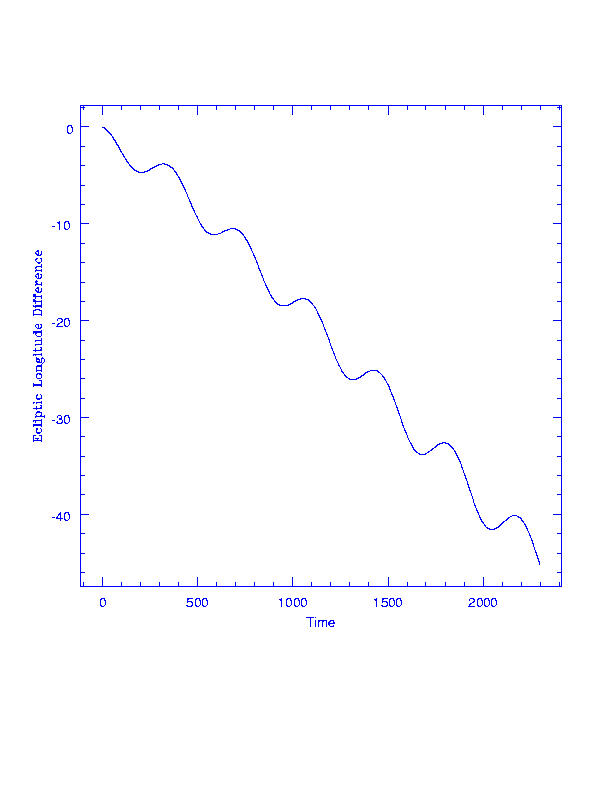
SIRTF trails Earth; longitude (deg) vs time (days). Every year it reaches its perihelion and speeds up a little, but on average it lags further and further behind. One degree of longitude is about 2.6 million km. The time axis runs from the year 2003 to 2009.
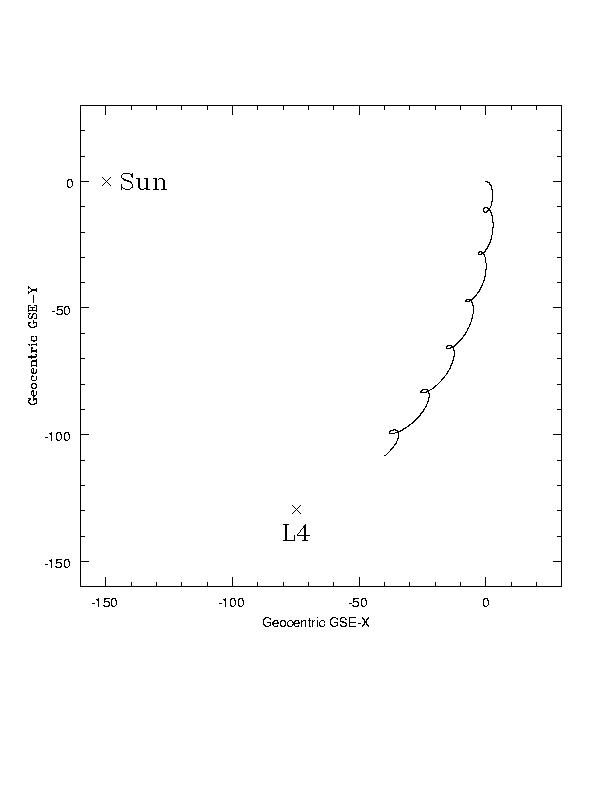
In a rotating frame, centered on the Earth where the Earth-Sun line is kept fixed, SIRTF makes little epicycles and heads towards Earth-Sun L4. Units are millions of km.
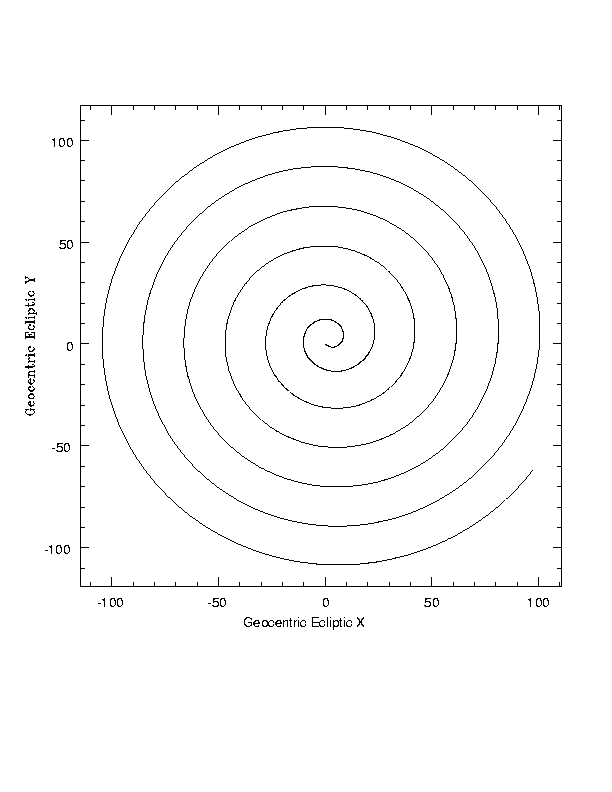
In an inertial frame centered on the Earth, in ecliptic coordinates, SIRTF makes a spiral outwards from the Earth. Units are millions of km.
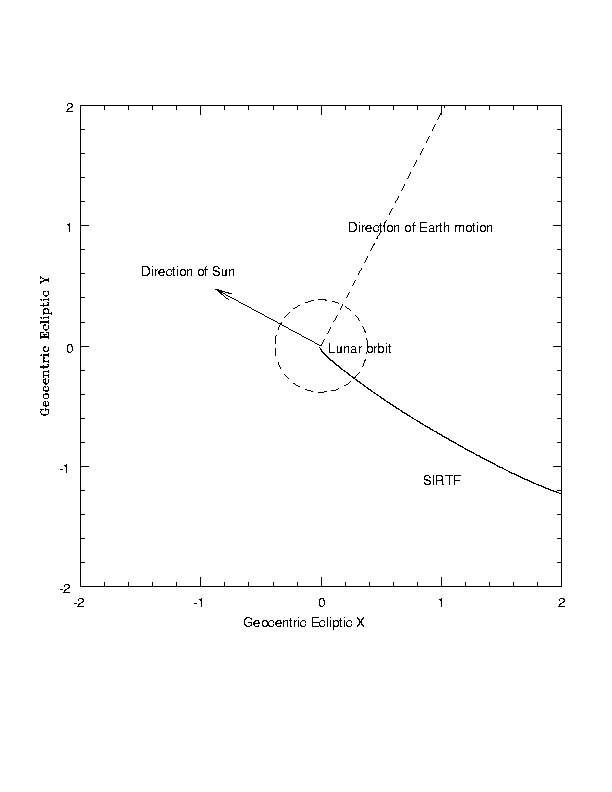
Zooming in on the previous figure we see that SIRTF sets off outward and backward relative to the Earth. At the time of launch the Moon is on the opposite side of its orbit from SIRTF's trajectory.
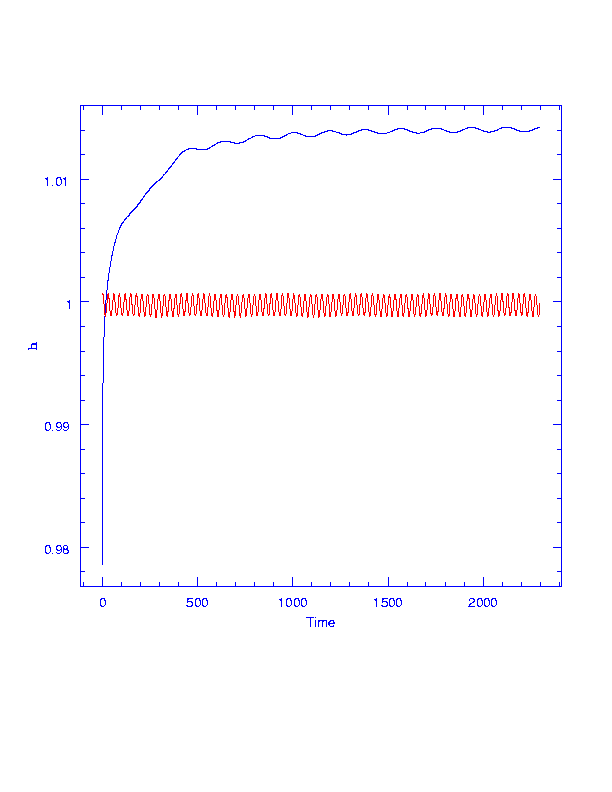
H = (h*h/GM), square of angular momentum (unit AU), vs time. See SIRTF gain angular momentum from the Earth thanks to the magic of the three-body problem. Earth is in red, bouncing around the Earth-Moon barycenter.
In the two-body problem, the specific angular momentum r * v = h is a constant (Kepler's second law),such that (r*v)**2 / GM = a(1-e*e), where a is the semimajor axis and e is the eccentricity. Since these orbits are nearly circular, e is almost zero and (r*v)**2/GM is roughly the semimajor axis of the orbit around the Sun - if the Earth's gravity could be neglected. But in fact Earth, just ahead of SIRTF, tugs on it to give it extra speed around the Sun, and in the first few months converts SIRTF's orbit from one whose radius a is less than the Earth's to one in which the radius is just a bit bigger than the Earth's.